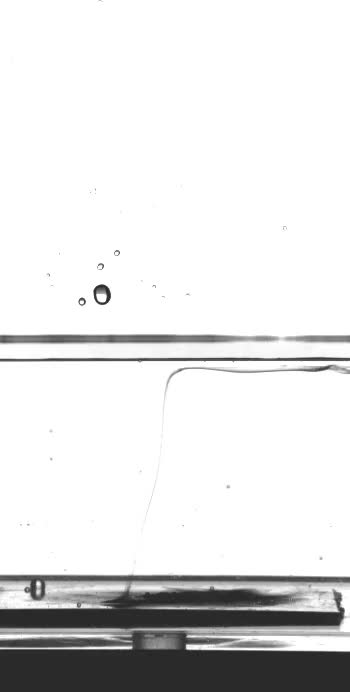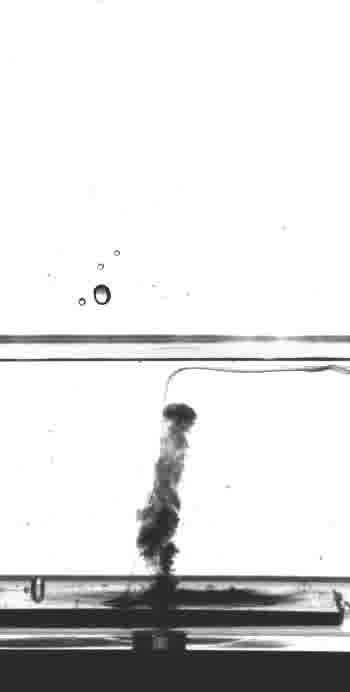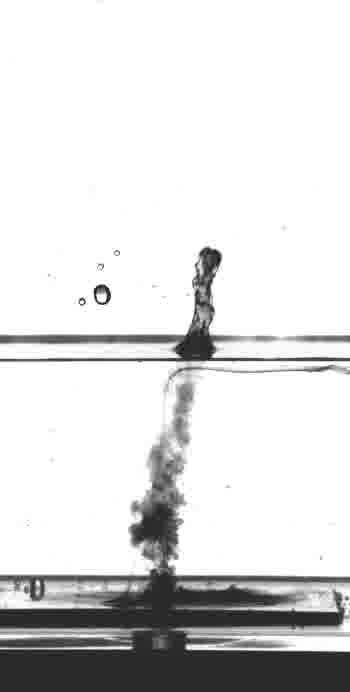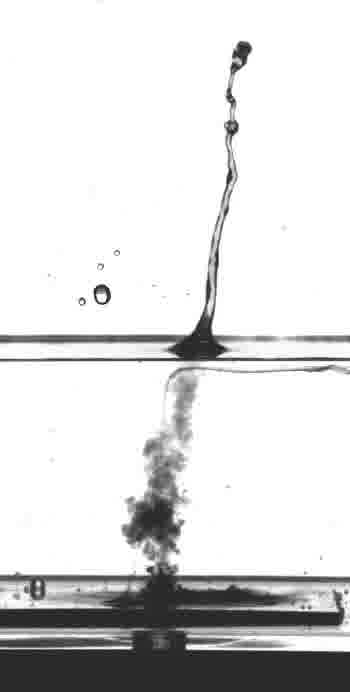
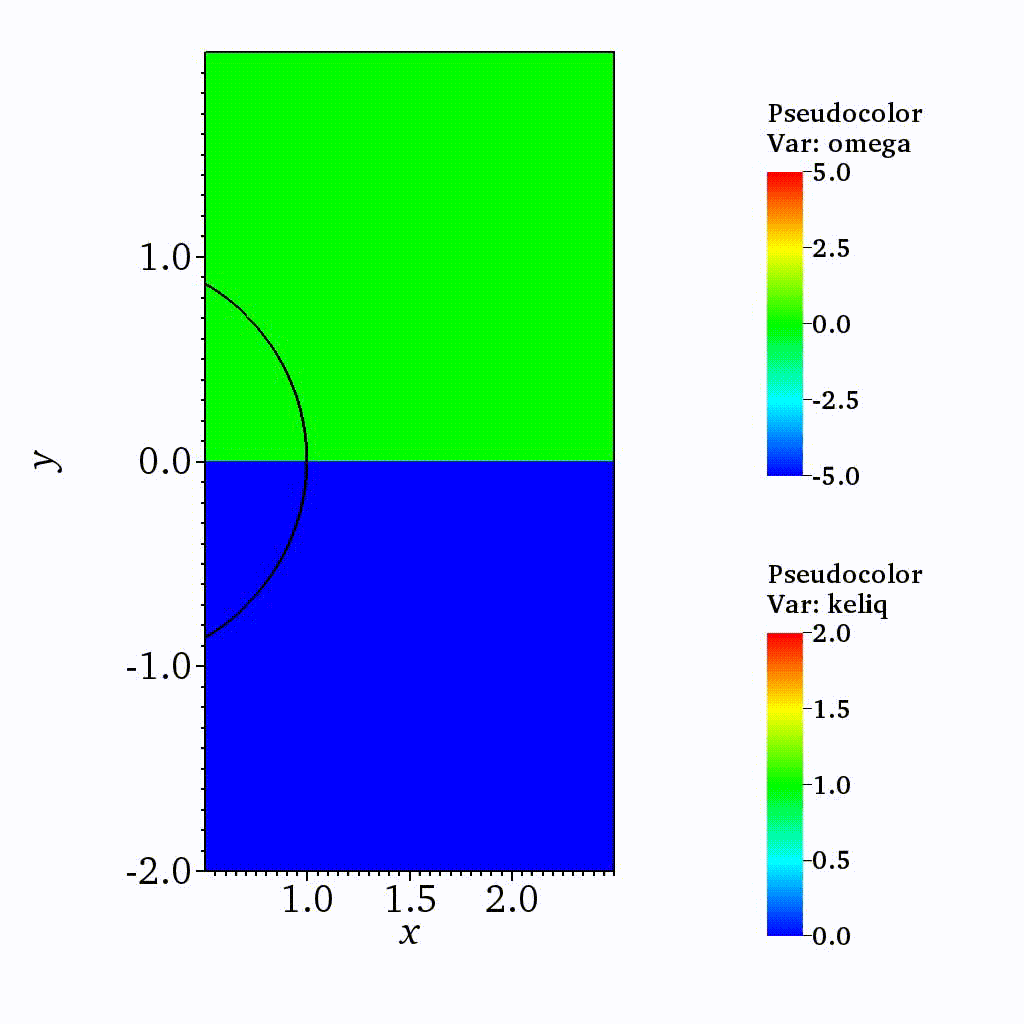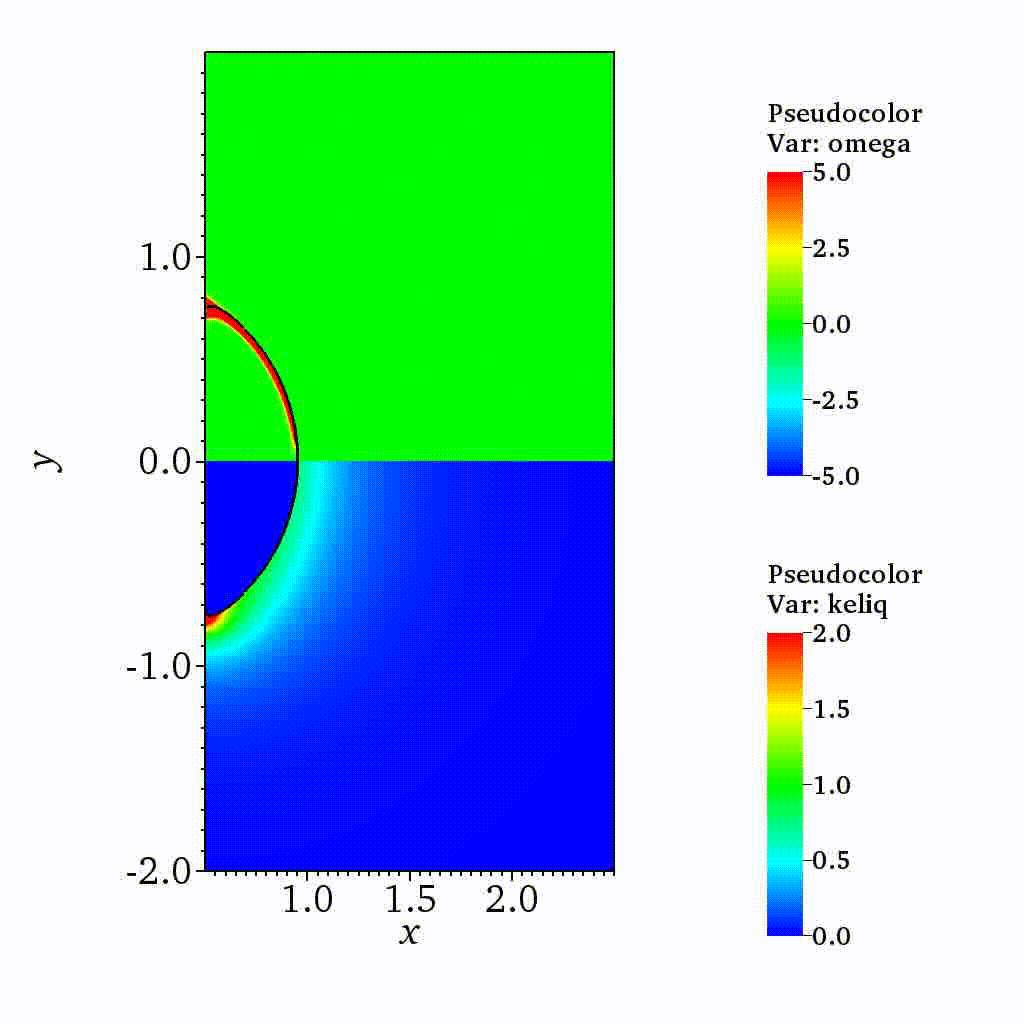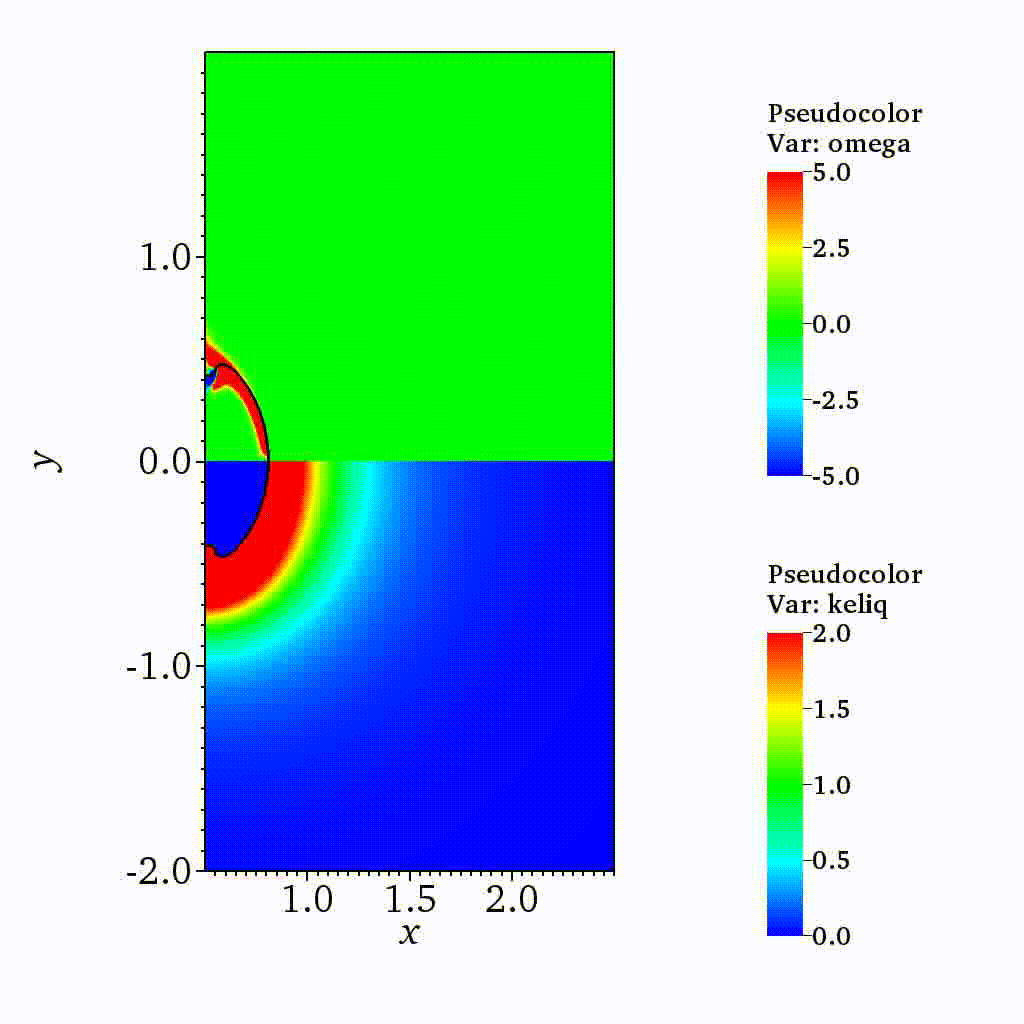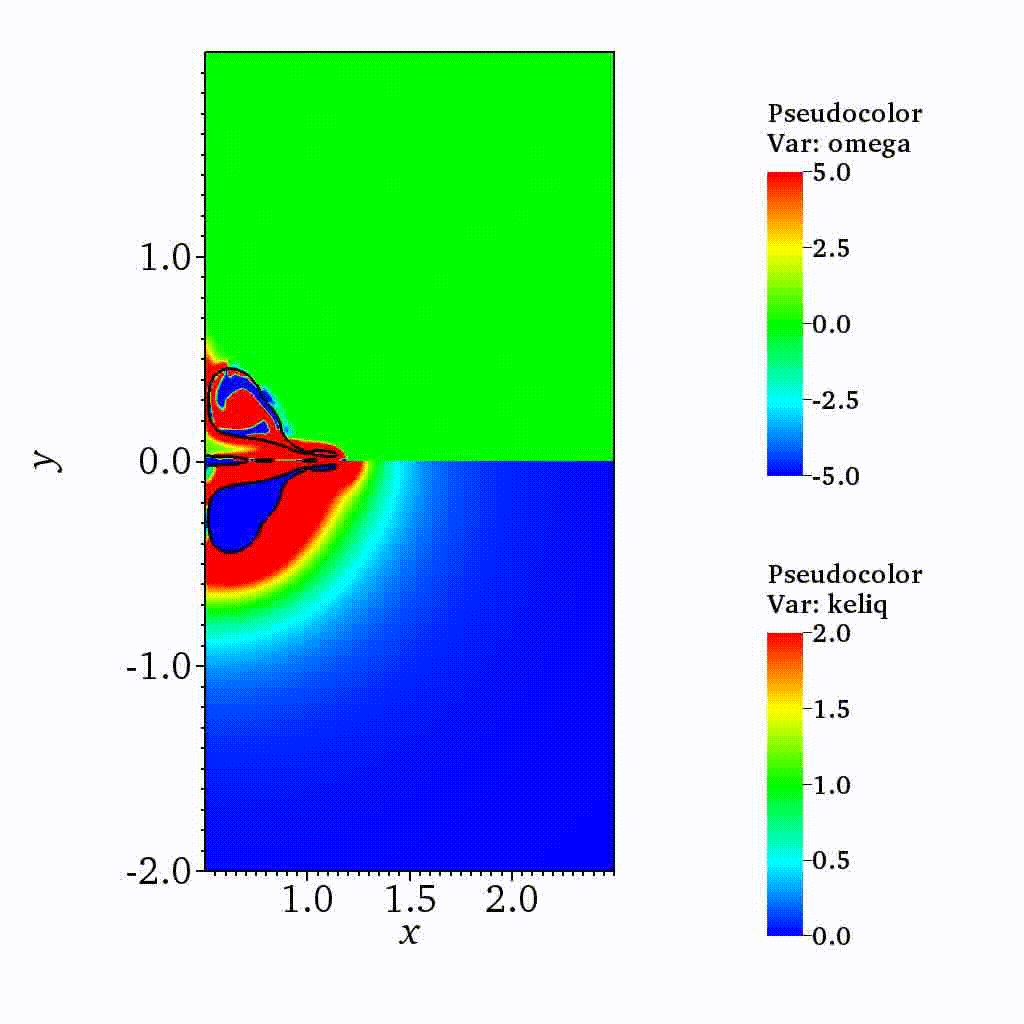
Cavitation
Cavitation and bubble dynamics are problems with many applications in engineering, acoustics, environmental sciences, etc... Check in the left menu some relevant works
PhDs: Mandeep Saini, Maya Daou, Elena Igualada (Carlos III Univ.)
Postdoctoral researchers: Lucas Prouvost, Luca Bergamasco
Research stages: Davide Preso (EPFL), Youssef Saade (Twente Univ), Yuzhe Fan (Harbin Univ)
Numerical Simulations
Associated publications
A Review of the Accuracy of Direct Numerical Simulation Tools for the Simulation of Non-Spherical Bubble Collapses (JIIS, 2024)
Direct numerical simulations of microlayer formation during heterogeneous bubble nucleation (JFM, 2024)
Finite speed of sound effects on asymmetry in multibubble cavitation (PRF, 2024)
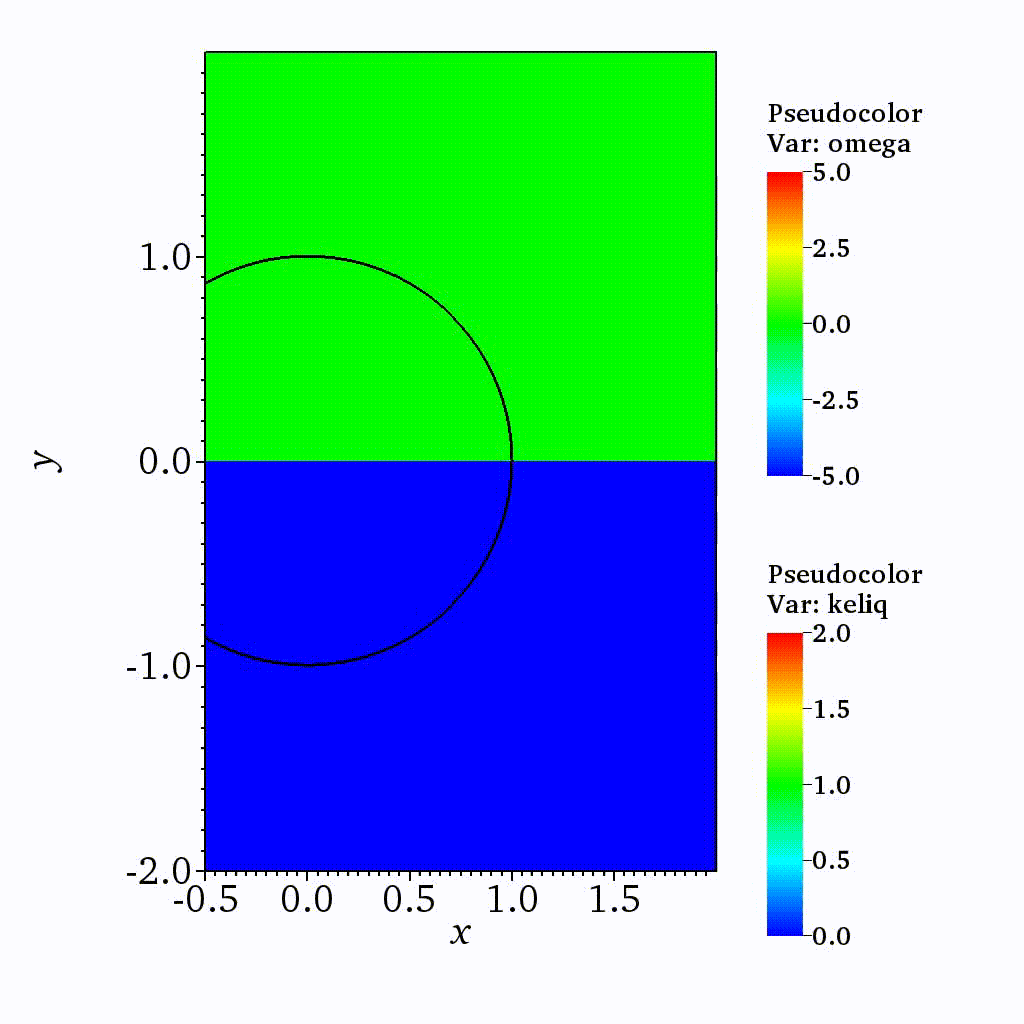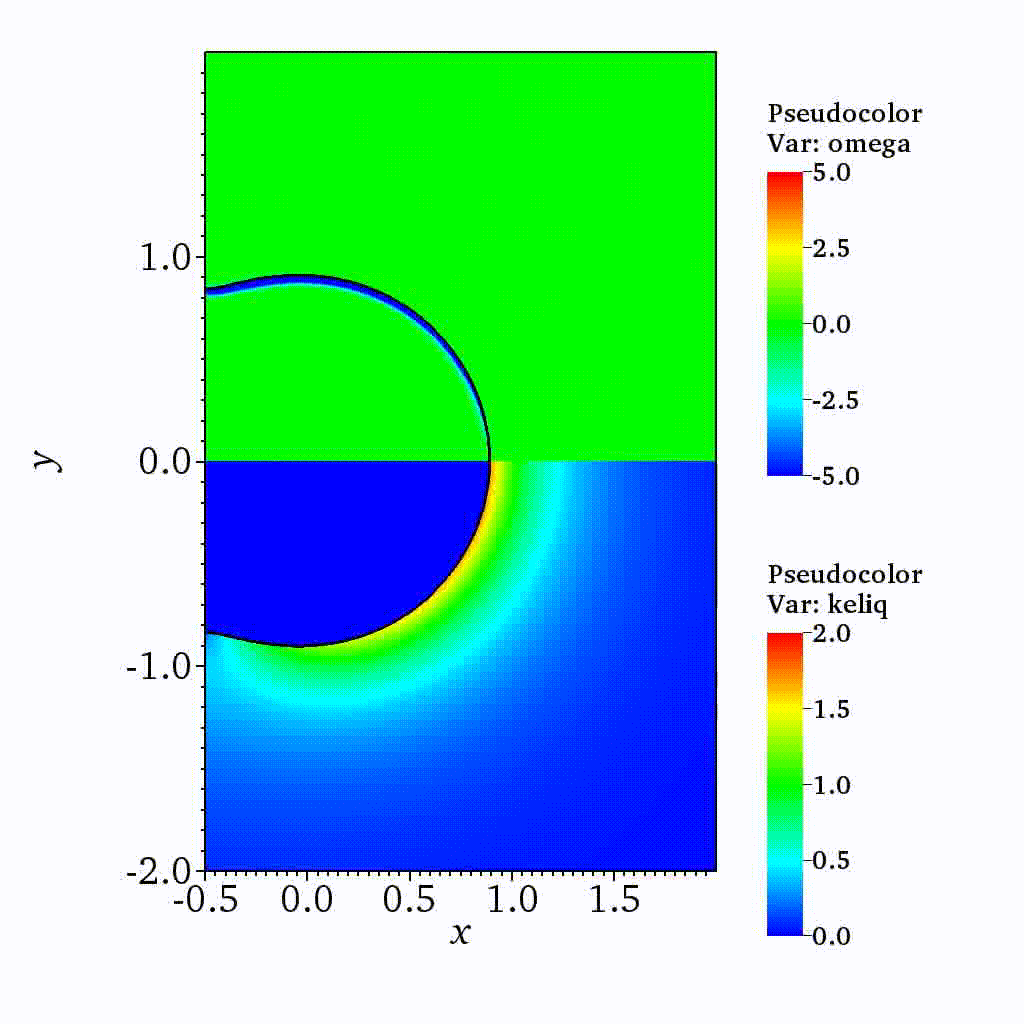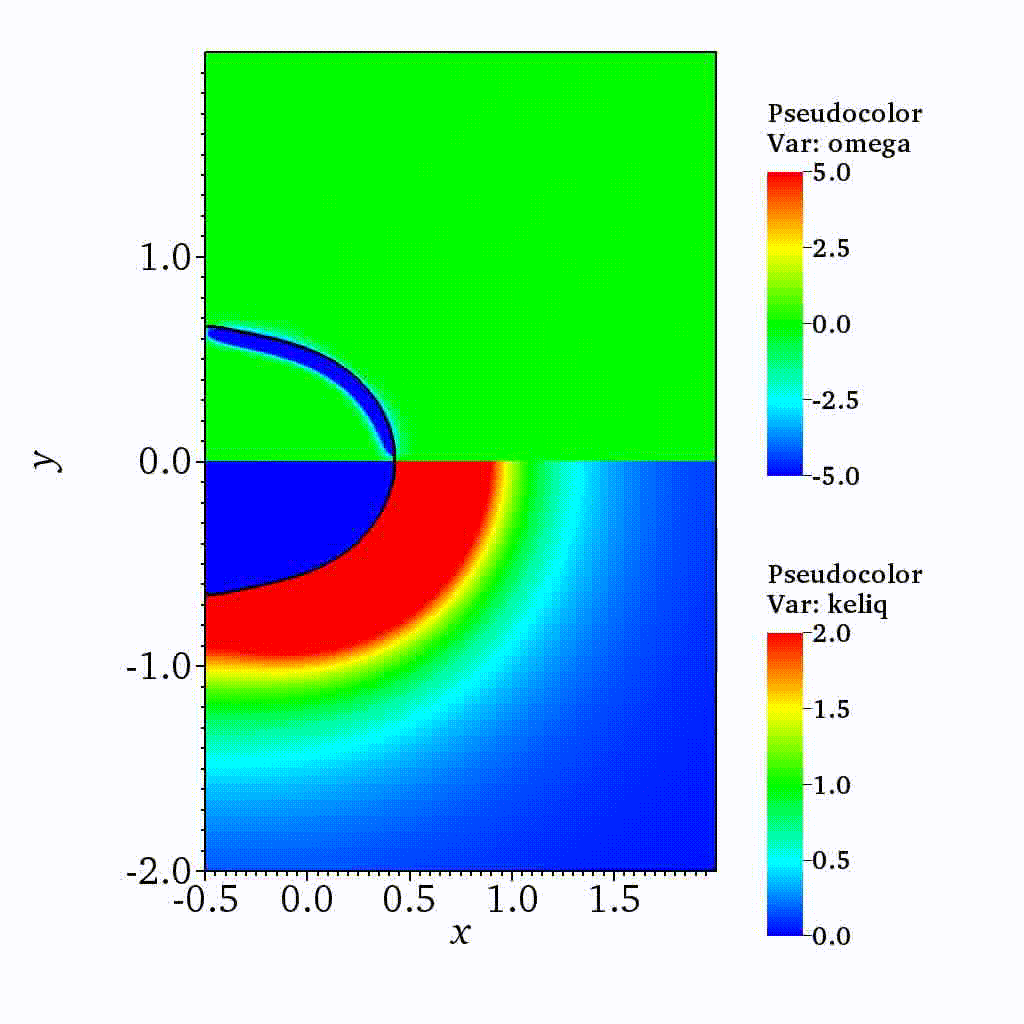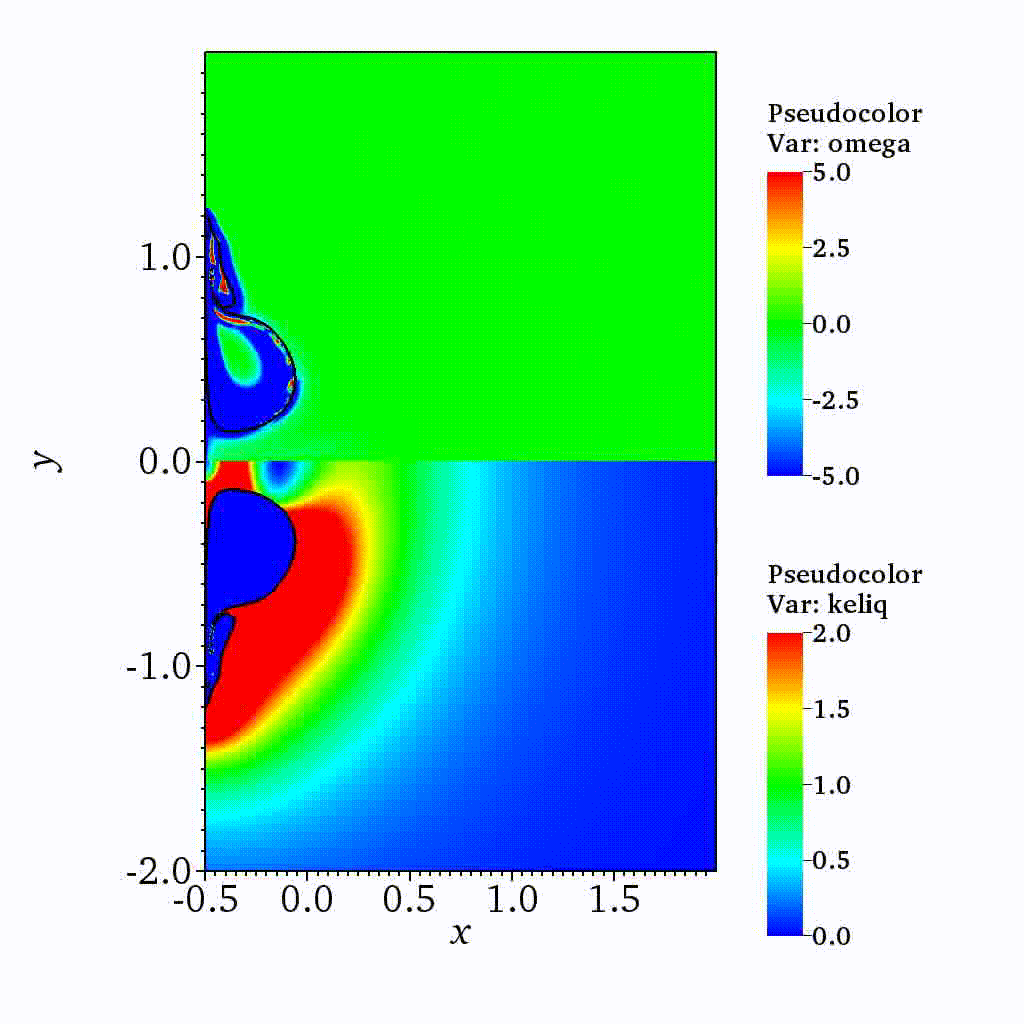
On the dynamics of a collapsing bubble in contact with a rigid wall (JFM, 2022)
Optimal subharmonic emission of stable bubble oscillations in a tube (PRE, 2020)
A Review of Models for Bubble Clusters in Cavitating Flows (JFTC, 2018).
Oscillation regimes of gas/vapor bubbles (IJHMT, 2017)
Modelling bubble clusters in compressible liquids [JFM, 2011]
Liquid compressibility effects during the collapse of a single cavitating bubble [JASA, 2011]
Influence of the accommodation coefficient on nonlinear bubble oscillations [JASA, 2010]
Dynamics of a single cavitating and reacting bubble [PRE, 2007]
Acoustics
Regressing bubble cluster dynamics as a disordered many-body system (JFM, 2024)
Time-delayed interactions on acoustically driven bubbly screens (JASA, 2021)
Optimal Control of SonoVue Microbubbles to Estimate Hydrostatic Pressure (T-UFFC, 2019)
Nonlinear acoustic propagation in bubbly liquids: Multiple scattering, softening and hardening phenomena (JASA, 2016)
Mass transfer effects on linear wave propagation in diluted bubbly liquids (JFM, 2015)
Effect of direct bubble-bubble interactions on linear wave propagation in bubbly liquids (PRE, 2014)
Experimental
Finite amplitude wave propagation through bubbly fluids (IJMF, 2024)
Vapor compression and energy dissipation in a collapsing laser-induced bubble (PoF, 2024)
Shock propagation effects in multilayer assembly including a liquid phase (KEM, 2017).
Investigation of the collapse of bubbles after the impact of a piston on a liquid free surface (AIChE, 2017).
Physics of beer tapping (PRL, 2014)
Stability of bubbly liquids and its connection to the process of cavitation inception (PoF, 2014)